〓　熱に関する諸量　〓 .

◇温度 [K]　熱量 [J]　cal/J~4.18　J/cal~0.239　W=J/sec

■ 熱流量(単位面積、単位時間あたり) <h> [W/m^2]

■ 熱伝導率 K (W/m^2)/(K/m)=W/(m*K)

■ 熱量(単位体積あたり) q [J/m^3]

■ 比熱(単位体積あたり) Cv [J/(m^3*K)]　1K上げるのに必要な熱量

■ 拡散定数 D=K/Cv　[m^2/sec]

■ 熱源からの熱量(単位時間、単位体積あたり) s [W/m^3)]

■ 熱源の内部エネルギー(単位体積あたり) u [J/m^3]

〓　簡単なポアソン方程式　〓 .

■

〓　円柱形の熱源　〓 .

●△f(r.)=k　f(r.)=(1/4)*k*r.^2+C1*ln(r.)+C2

■ 円柱形の熱源　円柱全体に熱源量 s　熱伝導率 K　温度 T=T(r.)

　△T(r.)=-s/K　T(r.)=T(0)-(1/4)*(s/K)*r.^2　r.=0 で発散しないように

{計算例}r.=1.6*Ten(-2) m　K=22.5 W/(mK)

電熱線　1mあたり　電圧 5V　抵抗 7*Ten(-7)　s=(25/7)*Ten(7) W/m^3

　T(0)-T(r)
=(1/4)*(s/K)*r.^2
=(25/7)*Ten(7)*[1.6*Ten(-2)]^2/(4*22.5)
~102

▲中心の温度は、表面より100度ほど高い{!}

〓　円柱形の熱源2　〓 .

●△f(r.)=-k*δ2(z)　f(r.)=-[1/(2Pi)]*k*ln(r.)　※Δln(r.)=+2Pi*δ2(r.)

◎円柱の軸にだけ熱源がある場合の温度分布

■ 熱源からの熱の総量(円柱の軸の単位長さあたり) G　温度 T=T(r.)

　△T(r.)=-(G/K)*δ2(z)

　T(r.)=-[1/(2Pi)]*(G/K)*ln(r.) ★

{苦労した!2012/3}{すっきりわかった!2013/8}

〓　円柱形の熱源3　〓 .

◎同心軸の円柱2つ　小さい円柱から大きい円柱に向かって、熱が流れ出る。2つの円柱間には熱源はない。

●△f(r.)=k　f(r.)=(1/4)*k*r.^2+C1*ln(r.)+C2　※△(r.^2)=4 △ln(r.)=0

◆ 小さい円柱(半径 a　温度 T1)　大きい円柱(半径 b　温度 T2)

その間の空間の熱伝導率 K

■ △T(r.)=0　T(r.)=C1*ln(r.)+C2 ★

境界条件を代入して、

　T1=C1*ln(a)+C2　T2=C1*ln(b)+C2　⇒

　T1-T2=C1*ln(a/b)　C1=-(T1-T2)/ln(b/a)=-(T1-T2)/[ln(b)-ln(a)]

　C2
=T1+(T1-T2)*ln(a)/ln(b/a)
=T1*[1+ln(a)/ln(b/a)]-T2*ln(a)/ln(b/a)
=[T1*ln(b)-T2*ln(a)]/[ln(b)-ln(a)]

　T(r.)*ln(b/a)
=-(T1-T2)*ln(r.)+[T1*ln(b)-T2*ln(a)]
　T(r.)=[T2*ln(r./a)-T1*ln(r./b)]/ln(b/a) ★

{別解}外側に流れ出ていく熱の総量(円柱の軸の単位長さあたり) G [W]

半径r (a<r<b) の円柱で包んで考えると、<h>=h*<ru>

　2Pi*r.*h=G　<h>=-K*<grad(T(r.))>=-<ru>*K*(T;r.)

　T;r.=-[G/(2Pi*K)]/r.　T(r.)=-[G/(2Pi*K)]*ln(r.)+C2

積分して　T1-T2=G*ln(b/a)/(2Pi*K) ★

　G=2Pi*K*(T1-T2)/ln(b/a)

〓　中心にだけ熱源がある球　〓 .

◎中心に熱源　その温度分布を求めよう。点電荷の電位の式を同じになる。

■ 熱源　単位時間あたり発生するエネルギー W [J/sec]　温度 T(r)

　△T(r)=-(W/K)*δ3(<r>)　T(r)=[1/(4Pi)]*(W/K)/r

〓　熱源が一様に分布した球　〓 .

◎熱源が一様に分布した球の、温度分布を求めよう。

◆ 半径 a　熱源からの単位時間、単位体積あたりの熱量 s [J/(sec*m^3)]

　温度 T=T(r)　△T(r<a)=-s/K　△T(r>a)=0

■ T(r<a)=-(1/6)*(s/K)*r^2+T(0) ★ 　※r=0 で発散しないように

　T(r>a)=C1/r ★ 　※r=∞ で T=0 になるように

後は、r=a で T と T;r が一致するようにして、

　-(1/6)*(s/K)*a^2+T(0)=C1/a　-(1/3)*(s/K)*a=-C1/a^2　⇒

　C1=(1/3)*(s/K)*a^3

　T(0)=(1/3)*(s/K)*a^2+(1/6)*(s/K)*a^2=(1/2)*(s/K)*a^2　⇒

　T(r<a)
=-(1/6)*(s/K)*r^2+(1/2)*(s/K)*a^2=(1/6)*(s/K)*(3*a^2-r^2) ★

　T(r>a)=(1/3)*(s/K)*a^3/r ★

表面で　T(a)=(1/3)*(s/K)*a^2 ★

中心で　T(0)/T(a)=1.5

球の内部で　T(r<a)/T(a)=3/2-(1/2)*(r/a)^2

球の外部で　T(r>a)/T(a)=1/(r/a)

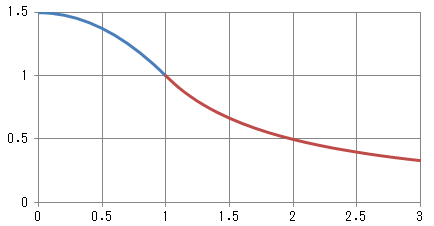
縦軸 T(r)/T(a)　横軸 r/a

グラフは、放物線と双曲線が繋がった形

{ポアソン方程式を勉強したら、すっきりわかった!2013/8}

〓　地球の熱伝導　〓 .

◎地球の熱伝導について調べよう。熱源が、地球全体に一様に広がっているとする。

●a=6.4*Ten(6) m　year/sec~3.16*Ten(7)

地球の熱エネルギー 8*Ten(20)_J/1年
=8*Ten(20)/[3.16*Ten(7)]
=2.53*Ten(13)_J/sec

　K=0.03 J/(cm*sec*K)=3 J/(m*sec*K)

◆ 熱流量(単位面積、単位時間あたり) <h>=-K*grad(T)

■ T(r<a)=(1/6)*(s/K)*(3*a^2-r^2)

　h(r)=-K*grad(T)=(1/3)*s*r　h(a)=(1/3)*s*a　s=3*h(a)/a

　4Pi*a^2*h(a)=2.53*Ten(13)

　h(a)
=2.53*Ten(13)/{4Pi*[6.4*Ten(6)]^2}
~0.05_W/m^2

　T(0)=(1/2)*(s/K)*a^2=(3/2)*h(a)*a/K

　T(0)-T(a)
=(1/2)*(s/K)*a^2-(1/3)*(s/K)*a^2
=(1/6)*(s/K)*a^2
=h(a)*a/(2*K)
=0.05*6.4*Ten(6)/(2*3)
~5万_K

※地球の中心温度 6000_K