☆ 絶対値の対数関数 ☆
◎ log ln ネイピア数 e ln|x| {理解が不十分!使えていないなあ!2015/7} ★_
【表記のお約束】 10^x=Ten(x) 微分
; 時間微分
' 積分 $
ベクトル <A> 単位ベクトル
<-u> 座標単位ベクトル
<x> 内積
* 外積 #
ネイピア数 e 虚数単位
i e^(i*x)=exp(i*x)=expi(x)
〓 対数関数 〓
■ log(a,x)=[a を何乗すると x になるか]
log(a,a^x)=x a^log(a,x)=x
■ log(10,x)=LOG(x) log(e,x)=ln(x)〔 e:ネイピア数 〕
〓 指数法則 〓
■ a^m*a^n=a^(m+n) (a*b)^m=(a^m)*(a^n) (a^m)^n=a^(m*n)
〓 対数の性質 〓
■ 底 a のとき log(a,x*y)=log(a,x)+log(a,y) log(a,x^p)=p*log(a,x)
■ 底 e のとき ln(x*y)=ln(x)+ln(y) ln(x^p)=p*ln(x)
■ 底 10 のとき LOG(x*y)=LOG(x)+LOG(y) LOG(x^p)=p*LOG(x)
〓 関数 y=ln|x| 〓
■ 関数 y=ln(x) 〔x,y:実数〕
exp(y)=x x>0 であるから、ln(x) は x≦0 で、定義できない
それに対して、x=0 以外の、すべての実数で定義できる次の関数を考える ln|x|

■ ln|x| を定義する
x>0 で y=ln|x|=ln(x) x=exp(y)
x<0 で y=ln|x|=ln(-x) -x=exp(y)
{ln|x| が出てきた、y軸対称であるグラフをイメージすればよいと思う!2015/9
〓 ln|x|の積分 〓
■【 ln|x| の積分 】
(x*ln|x|);x=(x;x)*ln|x|+x*(ln|x|;x)=ln|x|+x*(1/x)=ln|x|+1
(x*ln|x|-1);x=ln|x|
${ln|x|*dx}=x*ln|x|-1 ★
|
● ln|x|;x=1/x ${(1/x)*dx}=ln|x| ${ln|x|*dx}=x*ln|x|-1 |
〓 lim[x→0]{x^x} ? 〓
◎ lim[x→0]{x^x}=0 にならない
■ lim[x→0]{x}=0 lim[x→0]{ln(x)}=-∞
lim[x→0]{x*ln(x)}=0*(-∞)=?
x=0.1 のとき x*ln(x)=-0.230 x=0.01 のとき x*ln(x)=-0.046

■ 2^x と x^2 を比べる
|
x |
0.01 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
2 |
|
2^x |
1 |
1.07 |
1.15 |
1.23 |
1.32 |
1.41 |
1.52 |
1.62 |
1.74 |
1.87 |
2 |
4 |
|
x^2 |
0.001 |
0.01 |
0.04 |
0.09 |
0.16 |
0.25 |
0.36 |
0.49 |
0.64 |
0.81 |
1 |
4 |
x→+0 で より早く小さくなるのは x^2
■ x^x と ln(x^x)=x*ln(x) を 求める
|
x |
0.01 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
2 |
|
x^x |
0.95 |
0.79 |
0.72 |
0.70 |
0.69 |
0.70 |
0.74 |
0.78 |
0.84 |
0.91 |
1 |
4 |
|
x*ln(x) |
-0.05 |
-0.23 |
-0.32 |
-0.36 |
-0.37 |
-0.35 |
-0.31 |
-0.25 |
-0.18 |
-0.09 |
0 |
1.39 |
x → +0 で x → +0 ln(x) → -∞ x*ln(x) は x → +0 の効果が勝って、
x*ln(x) → -0 したがって x → +0 で x^x=1
lim[x→0]{x^x}=1 ★.{不思議!知らなかった!2016/7}
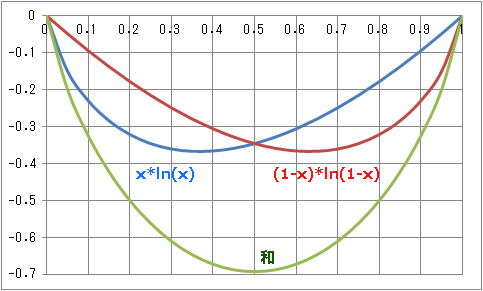
■《 x*ln(x) の最小値 》
y=x*ln(x)
y;x=ln(x)+1
y;x=0 を解くと ln(x)+1=0 ln(x)=-1
x=exp(-1)=1/exp(1)=1/e=1/2.7183=0.37
そのとき y=(1/e)*ln(1/e)=-1/e=-0.37
≫ x*ln(x) の最小値 -1/e=-0.37 〔x=1/e=0.37 のとき〕 ★.
■《 x^x の最小値 》
x=1/e~0.37 のとき 最小値=exp(-1/e)~0.69
■《 x*ln(x)+(1-x)*ln(1-x) の最小値 》
x=0.5 のとき 最小値=0.5*ln(0.5)+(1-0.5)*ln(1-0.5)=ln(0.5)=-ln(2)~-0.69
|
『x*ln(x)』 2016/7
■ x=1/e~0.37 のとき x*ln(x) の最小値=-1/e~-0.37 ■ x=0.5 のとき x*ln(x)+(1-x)*ln(1-x) の最小値=-ln(2)~-0.69 ■ x=1/e~0.37 のとき x^x の最小値=exp(-1/e)~0.69 |
■
〓 LOG(2) を求める 〓
◎ LOG(2)=log(10(2) の近似値を求める
● ln_10(2)=ln(2)/ln(10)~0.69315/2.3026~0.30103
■ 無理数を求める計算から root(10)~3.162 root(3.162)~1.778 などと求める事ができる。これは、10^(1/2) , 10^(1/4) を求める事と同じである。以下、繰り返せば、
|
x |
1/2 |
1/4 |
1/8 |
1/16 |
1/32 |
1/64 |
1/128 |
1/256 |
1/512 |
1/1024 |
LOG(y) |
|
10^x |
3.162 |
1.778 |
1.334 |
1.155 |
1.075 |
1.037 |
1.018 |
1.009 |
1.005 |
1.002 |
y |
この表を利用して、LOG(2) を求める。
表より LOG(1.778)=1/4 , LOG(3.162)=1/2
1/4<LOG(2)<1/2
■ a,b,c は上記の表の 10^x の値 2~a*b*c と近似できたとしよう
LOG(2)=LOG(a*b*c)=LOG(a)+LOG(b)+LOG(c) ★.
※ 積の数は、いくつでも同じ
■ 上記の表の値の積で表す事を考える
2/1.778~1.125 1.125/1.075~1.047 1.047/1.037~1.010 1.010/1.009~1.00099
ここで 表にはない値
LOG(1.00099)=0.00099/ln(10)=0.00099/2.3026~0.00043
LOG(2)
=LOG(1.778)+LOG(1.075)+LOG(1.037)+LOG(1.009)+LOG(1.0000457)
=1/4+1/32+1/64+1/256+0.00002
=(64+8+4+1)/256+0.00043
=77/256+0.00043
=0.30078+0.00043
=0.30121
★.
〓 指数関数のグラフ 〓
◎ 指数関数のグラフを対数グラフに書く
◆ y=a*x^k
■ 対数をとると ln(y)=ln(a)+k*ln(x)
対数グラフで 縦軸 ln(y) 横軸 ln(x) をとれば、直線になる ★
{知らなかった!2015/8}
★ y=x^2 ln(y)=2*ln(x)
★ 反比例 y=a/x ln(y)=ln(a)-ln(x)