| ���������悤Uz���@����.���v�͊w |
2016/7�@Yuji.W |
|
���S���̃G���g���s�[�� |
�� �S���̐L�яk�݂v�͊w�I�Ɉ����@�G���g���s�[
�� �x�N�g��<A>�@�c�x�N�g��<A)�@�P�ʃx�N�g��<-u>�@����*�@�O��#�@����;x�@���Ԕ���'�@10^x=Ten(x)�@exp(i*x)=expi(x)�@���f��\z�@�����萔- ��.
| �����v�͊w�I�G���g���s�[�� |
���y �G���g���s�[�̒�` �z
�G�l���M�[ E�@��Ԑ� W(E)�@�{���c�}���萔 kB
�@{��`}�@�G���g���s�[�@S=kB*ln(W)
���y ���v�͊w�I���x�̒�` �z
�@{��`}�@���x�@T=1/(S;E)
| ���S���̏ꍇ�̐��� |
�� n>>1 �̂Ƃ��@ln(n!)=n*[ln(n)-1]�@����Ɂ@ln(n!)=n*ln(n) ��.
�� �S���@�\ �\ �\ �\ �\ �\�@�@�M�������
�@�@�@�@ �\ | �\ �\ | �\�@�@�Z���Ȃ�
�������q1�̃G�l���M�[ 0�@�Z�����q1�̃G�l���M�[ e
�S���q�� N�@�Z�����q���̐� n�@���̊��� h=n/N�@�S�G�l���M�[ E=n*e=N*h*e
���s �ꍇ�̐� �t
�@W=C(N,n)=N!/[n!*(N-n)!]
�@ln(W)=ln(N!)-ln(n!)-ln[(N-n)!]
����3���������Ƃ��A
�@
N �͏\���傫��
�A n ���\���傫��(N ���͏�����)
�B n �́AN
�ɋ߂Â��߂��Ȃ��BN-n ���\���傫��
�@ln(W)=N*ln(N)-n*ln(n)-(N-n)*ln(N-n)
n �̑���� h ���g���āA
�@ln(W)/N
=ln(N)-h*ln(N*h)-(1-h)*ln[N*(1-h)]
=ln(N)-h*[ln(N)+ln(h)]-(1-h)*[ln(N)+ln(1-h)]
=ln(N)-h*[ln(N)+ln(h)]-(1-h)*ln(N)-(1-h)*ln(1-h)
=-h*ln(h)-(1-h)*ln(1-h)
��@ln(W)=-N*[h*ln(h)+(1-h)*ln(1-h)] ��.
|
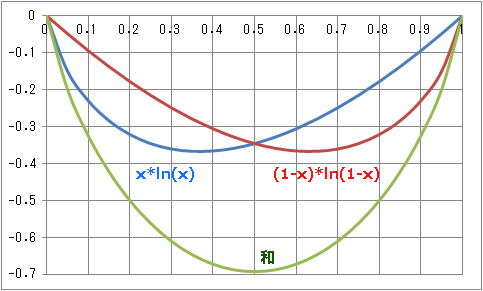
�wx*ln(x)�x�@2016/7
�� x=1/e~0.37 �̂Ƃ��@x*ln(x) �̍ŏ��l=-1/e~-0.37 �� x=0.5�@�̂Ƃ��@x*ln(x)+(1-x)*ln(1-x) �̍ŏ��l=-ln(2)~-0.69 �� x=1/e�@�̂Ƃ��@x^x �̍ŏ��l=exp(-1/e)~0.69 |
�� h=0.5�@�̂Ƃ��@�ő�l ln(W)~0.7*N�@���Ƃ�
���s ���� �t
�@[h*ln(h)];h=ln(h)+1
�@(1-h)*ln(1-h)=-ln(1-h)-1
�@[h*ln(h)+(1-h)*ln(1-h)];h=[ln(h)+1]-[ln(1-h)+1]=ln[(h/(1-h)] ��.
| ���S���̃G�l���M�[���z�� |
�� S=kB*ln(W)�@1/T=S;E�@���g���āA�S���̃G�l���M�[���z�����߂�
�� �G�l���M�[ E=N*h*e�@�G���g���s�[ S�@���x T
���s �G�l���M�[���z �t
�@S=kB*ln(W)=-N*kB*[h*ln(h)+(1-h)*ln(1-h)]�@S;h=-N*kB*ln[(h/(1-h)]
�@1/T=S;E=(S;h)/(E;h)={-N*kB*ln[(h/(1-h)]}/(N*e)=-(kB/e)*ln[(h/(1-h)]
h �� T �̊��Ƃ��ĕ\�����B
�@ln[h/(1-h)]=-e/(kB*T)
�@ln[(1-h)/h]=e/(kB*T)
�@(1-h)/h=exp[e/(kB*T)]
�@1-h=h*exp[e/(kB*T)]
�@1=h*{1+exp[e/(kB*T)]}
�@h=1/{1+exp[e/(kB*T)]}
h �� E �ŕ\���A
�@E=N*e/{1+exp[e/(kB*T)]} ��.
|
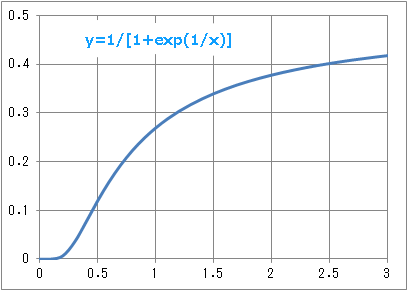
�w1/[1+exp(1/x)]�x�@2016/7
|
�� kB*T/e~0.5�@�̂Ƃ��@E/(N*e)~0.1
kB*T/e~1�@�̂Ƃ��@E/(N*e)~0.2
kB*T/e~2�@�̂Ƃ��@E/(N*e)~0.3
kB*T/e �� ���@�̂Ƃ��@E/(N*e)~0.5�@���x���オ���Ă��A�����قǂ̕��q�����A�Z�����q�ɂ͂Ȃ�Ȃ�
�@���@���v�͊w-�S���̃G���g���s�[�@���@