| ���������悤withUz���@����.�ʎq�͊w |
2016/2-2011/11�@Yuji.W |
|
���ʎq�͊w.���R���q.1������ |
�� ������͈͂���߂�ꂽ�ꍇ�@�ʎq�͊w�@1�����@�͂������Ȃ�
�� �v�����N�萔 h�@�f�B���b�N�萔 h.=h/(2*Pi)�@[�G�l���M�[*����]
��
�x�N�g��<A>�@���W�P�ʃx�N�g��<xu>�@�c�x�N�g��<A)�@����*�@�O��#
����;x�@���Ԕ���'�@10^x=Ten(x)�@exp(i*x)=expi(x)�@�k�����萔�l ��.
| ���ʎq�͊w.���R���q.1������ |
�� 1���q�������܂����S�G�l���M�[�����A�ʒu�G�l���M�[���萔
|
�w�V�����f�B���K�[�������x�@2015/10 �@ �V�����f�B���K�[�������@i*h.*[��(x,t);t]=[H]��(x,t) �A �����(���݊m�������ԂɈ˂�Ȃ��ꍇ)�@[H]��(x)=E*��(x) �B �Θ_.1����.�����.1�̗��q�@�͂��|�e���V�����ŕ\����(�d��Ȃ�) �@��(x);;x+(2*m/h.^2)*[E-V(x)]*��(x)=0 |
�� ���������^�������闱�q���A�ʎq�͊w�I�Ɉ���
�� �����܂����S�G�l���M�[ E �����������q�@���� m
�ʒu�G�l���M�[ V(x)=V0=�萔�@�̏ꍇ
�� �V�����f�B���K�[�������@��(x);;x=-[2*m*(E-V0)/h.^2]*��(x)
V0=0�@�̂Ƃ��@root(2*m*E)/h.��k0=���̒萔�@�ƒu���ƁA
�@��(x);;x=-k0^2*��(x)�@�@��{���@expi(k0*x) , expi(-k0*x)�@������ ��.
E>V0�@�̂Ƃ��@root[2*m*(E-V0)]/h.��k1=���̒萔�@�ƒu���ƁA
�@��(x);;x=-k1^2*��(x)�@�@��{���@expi(k1*x) , expi(-k1*x)�@������ ��.
E<V0�@�̂Ƃ��@root[2*m*(V0-E)]/h.��k2=���̒萔�@�ƒu���ƁA
�@��(x);;x=+k2^2*��(x)�@�@��{���@exp(k2*x) , expi(-k2*x)�@�w���� ��.
|
�w�ʎq�͊w.1����.���R���q�x�@2015/10 �� ���� m�@�S�G�l���M�[ E=�萔�@�ʒu�G�l���M�[ V(x)=V0=�萔�@ �@root(2*m*E)/h.��k0=���̒萔 �@root[2*m*(E-V0)]/h.��k1=���̒萔�@�� E-V0=�^���G�l���M�[ �@root[2*m*(V0-E)]/h.��k2=���̒萔 �� V0=0�@�̂Ƃ��@��{���@expi(k0*x) , expi(-k0*x)�@������ E>V0�@�̂Ƃ��@��{���@expi(k1*x) , expi(-k1*x)�@������ E<V0�@�̂Ƃ��@��{���@exp(k2*x) , exp(-k2*x)�@�w����(�ÓT�_�ł͑��݂��Ȃ�) |
{�������킩���ĂȂ�����!2015/10}
| ��������̈ʒu�G�l���M�[�Ɉ͂܂�Ă���ꍇ�� |
�� ���q�̓�����͈͂����������
|
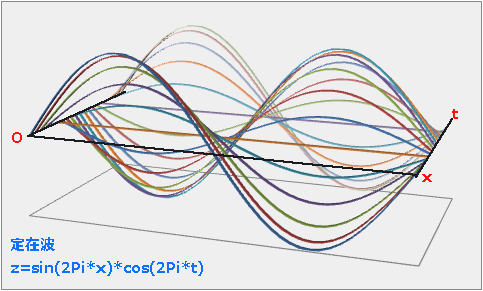
�w��ݔg.1�����x�@2015/9 �� ��ݔg�@x=0 , L �� z=0�@�g��(�ʑ�)���x v �� z(x,t)=z0*sin(k*x)*cos(w*t)�kn=�����@k=n*Pi/L�@w=k*v=n*Pi*v/L�l
|
�� 1���q��������͈͂� x=0~x=L�kL:���̒萔�l�Ƃ���
x=0 , x=L �̏��ŁA�ʒu�G�l���M�[�����̖�����ɂȂ�ƍl����B���̑��̈ʒu�ŁAV=0
x=0 , x=L �Ł@��(x)=0�@root(2*m*E)/h.��k0=���̒萔
�� [���� L �ɂ���g�̐�]=[k0/(2Pi)]*L
�g�͒��� 2*L �ɊԂɎ��R������Ƃ��ā@[k0/(2Pi)]*(2*L)=n�kn:���R���l
�@k0=n*Pi/L
�@��(x)=��0*sin(n*Pi*x/L) ��.
�� �������A�V�����f�B���K�[��������������
���̂Ƃ��@k(n)=n*Pi/L�@p(n)=n*Pi*h./L�@E(n)=n^2*[(Pi*h.)^2/(2*m)]/L^2 ��.
(�p)�g����G�l���M�[���A���� L �̊��ɂȂ��Ă��āA���R�Ȓl����鎖���ł��Ȃ�
��
${|��n(x)|^2*dx}[x:0~L]
=${|sin[n*(Pi/L)*x] |^2*dx}[x:0~L]
=(1/2)*L*1
=L/2�@������A
�K�i��������Ԋ� ��n(x)=root(2/L)*sin(n*Pi*x/L)�kn=���R���l ��.
| �����G�l���M�[�� |
�� �v�����N�萔 h=4.14*Ten(-21)_MeV*sec�@h*c=1.24*Ten(-6)_eV*m
�f�B���b�N�萔 h.=6.58*Ten(-22)_MeV*sec
@m=�d�q�̎���*c^2=�ÓT�d�q���a=2.8*Ten(-15)_m
1_MeV=1.60*Ten(-13)_J
�� �d�q�@m*c^2��@m=0.510_MeV
�@[(Pi*h.)^2/(2*m)]
=[(h/2)^2/(2*m)]
=[(h*c/2)^2/(2*@m)]=(h*c)^2/(8*@m)
�@[(Pi*h.)^2/(2*m)]
=(h*c)^2/(8*@m)
=[1.24*Ten(-6)]^2/{8*[0.51*Ten(6)]}
=3.77*Ten(-19)_eV*m^2
�� L=10_cm �̂Ƃ��@
�@���G�l���M�[ E(1)=[(Pi*h.)^2/(2*m)]/0.1^2=3.77*Ten(-17)_eV ��.
�����̌��q1�� 1_eV�@�e���r�d�g�̌��q1�� Ten(-9)_eV
�d�q�̃G�l���M�[�����U�I(�ƂтƂ�)�ł���ƌ����Ă��A���o�ł��Ȃ��B�A���ʂł���ƌ��Ȃ��Ă悢�����킩��B
�� �d�q���A���a��10�{�̒����ɕ����߂�@L=5.6*Ten(-14)_m
�@E(1)=[3.77*Ten(-19)]/[5.6*Ten(-14)]^2=1.20*Ten(8)_eV=120_MeV ��.
| �����݊m���� |
�� 1�̗��q�@���� m�@�ʒu�G�l���M�[ V=0�@����ԁ@���q�̓�����͈� x=0~L
��Ԋ� ��n(x)=root(2/L)*sin(n*Pi*x/L)
���q�� x=A~B �ɂ��鑶�݊m�� P(A~B)
|
�� ${sin(x)^2*dx}=x/2-sin(2*x)/4�@${sin(x)^2*dx}[x:0~Pi/2]=Pi/4 �� ${sin(a*x)^2*dx}=x/2-sin(2*a*x)/(4*a) �@${sin(a*x)^2*dx}[x:0~Pi/(2*a)]=Pi/(4*a) �� �� sin(x)^2 �� x=0~Pi ��6���������}�`�ʐς̔�@0~Pi �̖ʐς� 1 �Ƃ��āA �@�@3%�@�A17%�@�B30%�@�C30%�@�D17%�@�E3% |
|
�� ${sin(n*Pi*x/L)^2*dx}=x/2-sin(2*n*Pi*x/L)/(4*n*Pi/L) �� n:���� �̂Ƃ��@${sin(n*Pi*x/L)^2*dx}[x:0~L]=L/2 |
�� P(A~B)
=${|��n(x)|^2*dx}[x:A~B]
=(2/L)*${sin[n*(Pi/L)*x]^2*dx}[x:A~B]
=(2/L)*[x/2-sin(2*n*Pi*x/L)/(4*n*Pi/L)][x:A~B]
=x/L-sin(2*n*Pi*x/L)/(2*n*Pi)][x:A~B]
=(B-A)/L-[sin(2*n*Pi*B/L)-sin(2*n*Pi*A/L)]/(2*n*Pi)
��@P(A~B)=(B-A)/L-[sin(2*n*Pi*B/L)-sin(2*n*Pi*A/L)]/(2*n*Pi) ��.
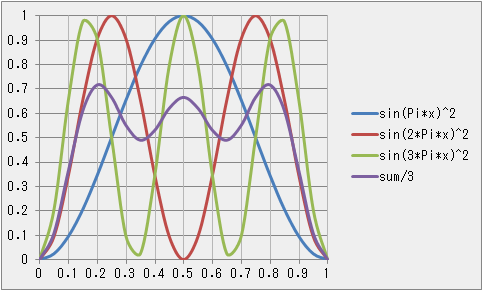
�� �� sin(x)^2 �� x=0~Pi ��6���������}�`�ʐς̔�@0~Pi �̖ʐς� 1 �Ƃ��āA
�@�@3%�@�A17%�@�B30%�@�C30%�@�D17%�@�E3%
x=L/3~2*L/3 �̑��݂���m��=60%
�� n=2 �̂Ƃ��@���E�Q�̕����̑��݊m�����傫���@�����t�߂͏�����
n=3 �̂Ƃ��@3�̈ʒu�ɂ��ڂ��Ă���
���̘a�@�[�ɂ��鑶�݊m���͏��������̂́A�����ԂȂ炳��Ă��āA�ʒu�ɂ���đ��݊m�������܂�ς��Ȃ��悤�ɂȂ��Ă���{�������낢!2015/9}
�� n=3 �̂Ƃ�
�@P(A~B)=(B-A)/L-[sin(6*Pi*B/L)-sin(6*Pi*A/L)]/(6*Pi)
�@P(L/12~L/4)=1/6-[-1-1]/(6*Pi)=1/6+1/(3*Pi)~0.17+0.11=0.28
| ���G�l���M�[�� |
�� ��n(x)=root(2/L)*sin(n*Pi*x/L)�kn=���R���l�@[H]=-[h.^2/(2*m)]*[;;x]
�� �G�l���M�[�̌ŗL�l�@
�@��n(x);;x=-(n*Pi/L)^2*root(2/L)*sin(n*Pi*x/L)=-(n*Pi/L)^2*��n(x)
�@[H]��n(x)
=-[h.^2/(2*m)]*��n(x);;x
=+[h.^2/(2*m)]*(n*Pi/L)]^2*��n(x)
=+[n^2*Pi^2*h.^2/(2*m*L^2)]*��n(x)
�@Pi^2*h.^2/(2*m*L^2)=E1�@�ƒu���ƁA
�@[H]��n(x)=+n^2*E1*��n(x)
�@En=n^2*E1 ��.
�� �G�l���M�[�̊��Ғl�@
�@��n(x)�̕��f������ ��n(x)!=root(2/L)*sin(n*Pi*x/L)=��n(x)
�@${|��n(x)|^2*dx}[x:0~L]=1�@����������A
�@@En
=${��n(x)!*[[H]��n(x)]*dx}[x:0~L]
=+[n^2*Pi^2*h.^2/(2*m*L^2)]*${|��n(x)|^2*dx}[x:0~L]
=n^2*Pi^2*h.^2/(2*m*L^2)
=E1*n^2 ��.
| ���ʒu�̕��ϒl�� |
�� ��n(x)=root(2/L)*sin(n*Pi*x/L)�kn=���R���l�@�ʒu�̕��ϒl @x(n)
�� |��n(x)|^2 �� x=L/2 �ɂ��Đ��Ώ̂�����@@x(n)=L/2
�� �v�Z�ŋ��߂悤
�@${|��n(x)|^2*dx}[x:0~L]=1�@������A
�@@x(n)
=${��n(x)!*[x*��n(x)]*dx}[x:0~L]
=${x*��n(x)^2*dx}[x:0~L]
=(2/L)*${x*sin(n*Pi*x/L)^2*dx}[x:0~L]
|
�� ${x*sin(k*x)^2*dx} �܂��@sin(k*x)^2=[1-cos(k*x)]/2�@���g���āA �@${x*sin(k*x)^2*dx}=(1/2)*${[x-x*cos(k*x)]*dx} ��1���@${x*dx}=x^2/2 ��2���@${x*cos(k*x)]*dx} �@${x*sin(k*x)^2*dx}=x^2/4-x*sin(k*x)/(4*k)-cos(k*x)/(2*k^2) |
�@${x*sin(n*Pi*x/L)^2*dx}
=x^2/4-x*sin(n*Pi*x/L)/(4*n*Pi/L)-cos(n*Pi*x/L)/(2*n^2*Pi^2/L^2)
�@${x*sin(n*Pi*x/L)^2*dx}[x:0~L]
=L^2/4-1/(2*n^2*Pi^2/L^2)+1/(2*n^2*Pi^2/L^2)
=L^2/4
�@@x(n)=(2/L)*(L^2/4)=L/2 ��.{�f���炵��!2015/9}
| ���� x*cos(x)�� |

�� �@�@y=x�@�A���@y=cos(x)
�B�@y=x*cos(x)�@�E�ɂ����ɂ�A�R�T�C���J�[�u�̐U�����A����傫���Ȃ��Ă����B
�C�ԁ@�� y=x*cos(x) ���Ax=0 ����Ax �̂��̒l�܂ł𐔒l�ϕ����ċ��߂��l���A�~�����{�������́B�ϕ��́A���̃O���t�ƁAx���Ƃ̊Ԃ̐}�`�̖ʐς�\���B�������Ax������ɂ���v���X�A���ɂ���ƃ}�C�i�X�ɂȂ�B
�� x=0~0.5�@�̃O���t��x������ɂ���̂ŁA���̐ϕ��l(��)�̓v���X
x=0~1�@�̃O���t��x����艺�̕������Ax������̕������A�L���̂ŁA���̐ϕ��l(��)�̓}�C�i�X
x=0~1.5�@�ϕ��l�́A�ɏ��l
x=0~2�@�̃O���t��x����艺�̕������Ax������̕����Ɠ����ʐςɂȂ�̂ŁA���̐ϕ��l(��)��0
����ɁA���l�Ȏ����N����Bx=�Q�A�S�A6 �̎��A�ϕ��l�� 0 �ɂȂ�B
| ���ʎq�͊w.1������ |
|
�w�V�����f�B���K�[������.1����.�Θ_.1�̗��q.���ԂɈˑ����Ȃ��x�@2015/9 �� �v�����N�萔 h�@�f�B���b�N�萔 h.=h/2Pi �� 1�̗��q�@���� m�@�ʒu�G�l���M�[ V(x)�@��Ԋ� ��(x,t) �@(�p)�g�� k=p/h.�@�p�U���� w=E/h. �@E=p^2/(2*m)+V�@[H]=-[h.^2/(2*m)]*[;;x]+V(x) �����(���݊m�������ԂɈ˂�Ȃ��ꍇ)�@��(x,t)=��(x)*expi(-w*t) �� ��(x);;x+(2*m/h.^2)*[E-V(x)]*��(x)=0 |
�� �͂������Ȃ����q�̉^���@�ʒu�G�l���M�[ V=0
�@��(x,t)=A*expi(k*x)*expi(-w*t)=A*expi(k*x-w*t)�@�Ɖ��肷��
�@[H]=-[h.^2/(2*m)]*[;;x]
�� �V�����f�B���K�[�������@��(x);;x+(2*m*E/h.^2)*��(x)=0
(�p)�g�����g���ĕ\���ƁA{�Ƃ��Ă��ȒP�ɂȂ�!}
�@��(x);;x+k^2*��(x)=0 ��.
���͊ȒP�ɋ��߂邱�Ƃ��ł��āA
�@��(x)=expi(k*x)
�@��(x,t)=expi(k*x)*expi(-w*t)=expi(k*x-w*t)=expi[(p/h.)*x-(E/h.)*t] ��.
{�V�����f�B���K�[�������̉����āA�ƂĂ�������Ɍ����邯�ǁA�����A���ʂ̔g�̕��f�w���\���� k �� w ���AE,p,h. �ŕ\��������!2013/4}
�� ���̎��R���q�̃G�l���M�[�A�^���ʂ����߂悤�B
�� i*h.*��(x,t);t=+h.*w*��(x,t)=+E*��(x,t)�@E ���G�l���M�[��\��
�@-i*h.*��(x,t);x=+h.*k*��(x,t)=+p*��(x,t)�@p ���^���ʂ�\��
�@���@�ʎq�͊w.���R���q.1�����@���@