�� 1��]�P�Ђ˂� ��
�� �o�X�P�b�g�{�[���̉�]�@�̑����Z�̉�]�@1��]1�Ђ˂�@���[���T���g�@�n���̉�] ��_�k�����萔�l
�y�x�N�g���z<A>�@�P�ʃx�N�g�� <-u>�@���� *�@�O�� #�@���W�P��<x>,<y>,<z>
�@�~�����W <r.u>,<au>,<z>�@�����W <ru>,<au>,<bu>
�y�ݏ�z3^2=9�@10^x=Ten(x)�@�y���ρzx������ f(x);x�@���Ԕ��� '�@�ϕ� $
�y�l�C�s�A��e�ze^x=exp(x)�@�ΐ� log(a,x)�@log(e,x)=ln(x)�@log(10,x)=LOG(x)
�y�����P��i�zi^2=-1�@e^(i*x)=exp(i*x)=expi(x)�@���f��z�̋��f�� \z
���@�o�X�P�b�g�{�[���̉�]�@�� .
�� ���d�͋�ԂɃo�X�P�b�g�{�[��������B
�{�[���̉�����˂��ĉ�]�������@<w1>=<x>*w�@
�{�[���̉E�����͂œ˂��Ɓ@<w2>=<y>*w
�{�[���̉����ƉE�����ɓ˂��ƁA
�@<w1>+<w2>=(<x>+<y>)*w�@�@|<w1>+<w2>|=root2*w
��]��:x����y���̓���(��45�x)
�� �Q�̉�]�� <x>,<y> �͋�ԓI�ɌŒ肳��Ă���B
���@�̑����Z�̉�]�@�� .
�� �o�X�P�b�g�{�[���̉�]�Ƃ͈قȂ�B
�� 2�̉�]��
�@
�ւ��̕ӂ��ʂ��č��E�ɐ����Ȏ� ������
�A
��-�ւ��̕ӂ�-�� �����ԉ�]�� �Ђ˂莲
�u1��]1�Ђ˂�v
�u1��]�v����������]���ɂ���B�O�]���]�B
�u1�Ђ˂�v�Ђ˂莲����]���ɂ���B
�������͋�ԏ�A�Œ肳��Ă���B�Ђ˂莲�́A���̂��̂��̂��A�������̎������]���Ă���B�o�X�P�b�g�{�[���̉�]�ƁA�̑����Z�̉�]�Ƃ́A�قȂ�B
���@�n���̉�]�@�� .
�� �̑����Z�́u1��]1�Ђ˂�v�̂悤�ɒn������]������A�n���̕\�ʂ͂ǂ̂悤�ɓ������낤���B�n�������]���̎����1��]����ԂɁA���̎��]�����������̎����1��]����ꍇ���l����B
�� �n������]������B�k�ɂ��ŏ���O�ɗ���悤�ɉ�]�����A���ɁA�^���A�^���A���ɖ߂�悤�ɉ�]����B���̂Ƃ��ɁA�����p���x�łЂ˂��������A���Ȃ킿�A���ʂ̒n���̎��]��������B1��]�P�Ђ˂�ł���B45�x���A����]�������}������Ă݂��B�k�ɁA�C���h������A�����m�̐^���A�ǂ��ړ����邩���������B
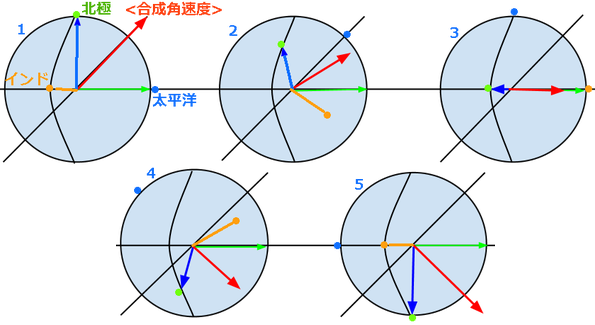
�� �e�n�_�̓���
�k��(��)�́A��O�A����ɐ^���Ɉړ�����B
�C���h(��)�́A���]���Ȃ���Γ�ɂ̈ʒu�ɂ������A�Ђ˂肪�����̂ŁA���E���Ɉړ��������ƁA�E���ɂ����B���̂��ƁA�����ʂ�Ȃ���A���ɖ߂��Ă���B(����ɂ��̂��Ƃ́A������ʂ�A�����ɍs���A�߂��ė���B�S�̂Ƃ��āA8�̎���`���B)
�����m(��)�́A�P���ɁA�~�^��������悤�ɓ����A�^��A�����ւƈڂ�B
�� �p���x�x�N�g���̓���
�n���̎��]��(��)���A�^�ォ�珙�X�Ɏ�O�ɁA����ɁA���̕��Ɉړ�����B���̓�����\���p���x�x�N�g���́A �� �ł���B�������傫�����ς��Ȃ��B
���̓��������A���]��(��)�ł���]����B���̊p���x�x�N�g���́A�������ł���B���]�������p���x�x�N�g���́A���̕�����ς��Ă����B
�� 2�̊p���x�x�N�g�������������̂��A�����p���x�x�N�g�����ł���B
�n�߂́A�E��45°�������Ă���B�n�\�ʂŌ����A�n���C�����肩�A��������]���ɂȂ�B�����́A�ŏ��͓����Ȃ��B(�����Ȃ��̂́A�ŏ������B)
�p���x�x�N�g���́A���͕ω����Ȃ����A���]��\���p���x�x�N�g�����́A���̌�����ς���̂ŁA�����x�N�g�����A�E�ߏ��O�A�E����O�A�E�߉���O�A�E�߉�45°�ƌ�����ς���B
�n���̉�]&�Ђ˂�́A���̓����Ă��������x�N�g���̎���̉�]�ŕ\����Ă���B ��
�����p���x�x�N�g���́A�~����`���������1������B
���u��]&�Ђ˂�v�Ƃ������G�ȓ������A1�́A�p���x�x�N�g���ŕ\�����Ƃ��ł���̂��킩�����B�������A���̊p���x�x�N�g�����g���A��]����Ƃ����킯���B�~���^��������p���x�x�N�g�����\���^�����A���^���B ��
{�������ۂɎ�Ɏ����āA�\�ʂɈ�����A��]&�Ђ˂��������J��Ԃ����Ȃ��ƁA�{���ɂ͂킩��Ȃ��B���̒��A1���������Ă݂���A�킩���Ă����B�ŏ��ɋC�������̂́A�ŏ��A�n���C�����肪�S�R�����Ȃ��Ƃ������������B�ł��A�ǂ�ǂ����ƁA���̃n���C�������Ă��܂��B���炭������A�����Ȃ��_(�����x�N�g���̎��ɂȂ�_)���A���X�ɓ����Ă����A�����āA�~��`���̂��ƁA�킩�������B!2013/1/14}
���@�̑����Z�̉�]-2-�@�� .
�� �̑����Z�́u1��]1�Ђ˂�v�ƒn���́u1��]1�Ђ˂�v���ׂ�ƁA���̂悤�ɑΉ����Ă���B
�@��-�k�Ɂ@��-��Ɂ@�ւ�-�C���h�@���̍�-�����m
���Ƒ��́A������ƑO���1��]���邾���B
�ւ��́A�O���猩�Ă��8�̎���`���B���S�Ɍ�둤�ɍs���Ă��܂����͂Ȃ��B
���̍��́A�O���猩�Ă�ƁA���ꂢ�ȉ~��`���B
{�������낢�Ȃ�!2017/10}{����I��́A2017�N���E�I�茠�u���v�ŋ����_��!}