�� ���ʏ�̓_�̈ړ�-�s�� ��
�� �u���ʏ�̓_�̈ړ�-�s��v
�����a1�̋��ʏ�̓_�̈ړ����A�s��ōl����B
���] rotation�@���] revolution
�k�\���̂���140710�lcos(a)=Ca�@sin(b)=Sb�@tan(x)=Tx�@10^x=Ten(x)
�x�N�g��<>�@�P�ʃx�N�g��<-u>�@�c�x�N�g��<)�@����<>:x�@����*�@�O��#
e^(x)=exp(x)=E(x)�@e^(i*x)=expi(x)=Ei(x)�@����;x�@���Ԕ���'�@�����萔
| ����]�ړ��� |
�����a1�̉~����̓_�̈ړ����l����B(x,y,z) �� (\x,\y,\z)
��]�s�� [R]=[R11 R12 R13|R21 �c|�c R33]=<R1)&<R2)&<R3)
�@�ړ��O�@x*<xu>+y*<yu>+z*<zu>
�@�ړ���@x*<R1>+y*<R2>+z*<R3>
3�̊��x�N�g������镽�s�l�ӌ`�̑̐ρ@�ړ��O 1�@�ړ��� |[R]|
���ȉ��̏��������B
�@|[R]|=1�@�傫���͕ς��Ȃ�
�A|<R1)|=|<R2)|=|<R3)|=1�@��]���Ă��邾��������A�����͕ς��Ȃ�
�B<R1)*<R2)=<R2)*<R3)=<R3)*<R1)=0�@����������
�C<R1)#<R2)=<R3)
| ����]�s�� |
| �u��]�s��-���W������]���v �����_�𒆐S�Ƃ����]�ړ��@<\x \y \z)=[R]*<x y z) �����_�𒆐S�Ƃ��A���W�������Ƃ����]�ړ��@��]�p a �@��]��x���@[Rx(a)]=[1
..|. Ca -Sa|. Sa Ca]
�����W�������Ƃ��āA90°��] �@[Rx(90°)]=[1
..|.. -1|. 1 .]
|
| ��90°��]�� |
��[Rx(90°)]=[1 ..|.. -1|. 1 .]�@\x=x�@\y=-z�@\z=y
�@[Ry(90°)]=[.. 1|. 1 .|-1 ..]�@\x=z�@\y=y�@\z=-x
�@[Rz(90°)]=[. -1 .|1 ..|.. 1]�@\x=-y�@\y=x�@\z=z
��<�k��)=<.. 1)�@<�C���h)=<1 ..)�@<�����m)=<. 1 .)
�@[Rx(90°)]*<�k��)=[1
..|.. -1|. 1 .]*<.. 1)=<. -1 .)
�@[Rx(90°)]*<�C���h)=<1
..)=<�C���h)
�@[Rx(90°)]*<�����m)=<.. 1)=<�k��)
��[Rx(90°)]^2=[1
..|.. -1|. 1 .]^2=[1 ..|. -1 .|.. -1]
�@yz���ʏ�œ_�Ώ̈ړ�
�@[Ry(90°)]^2=[..
1|. 1 .|-1 ..]^2=[-1 ..|. 1 .|.. -1]
�@xz���ʏ�œ_�Ώ̈ړ�
�@[Rz(90°)]^2=[. -1 .|1 ..|.. 1]^2=[-1 ..|. -1 .|.. 1]
��[Rx(90°)]*[Ry(90°)]=[1
..|.. -1|. 1 .]*[.. 1|. 1 .|-1 ..]
=[.. 1|1 ..|. 1 .]�@\x=z�@\y=x�@\z=y
[Ry(90°)]*[Rx(90°)]=[..
1|. 1 .|-1 ..]*[1 ..|.. -1|. 1 .]
=[. 1 .|.. -1|-1 ..]�@\x=y�@\y=-z�@\z=-x
�@not{ [Rx(90°)]*[Ry(90°)]=[Ry(90°)]*[Rx(90°)] }
��[Rz(90°)]*[Rz(-90°)]=[.
-1 .|1 ..|.. 1]*[.
1 .|-1 . .|.. 1]
=[1 ..|. 1 .|.. 1]�@�ω��Ȃ��A���R
��[Ry(90°)]*[Rz(a)]*[Ry(-90°)]
=[..
1|. 1 .|-1 ..]*[Ca
-Sa .|Sa Ca .|.. 1]*[..
-1|. 1 .|1 ..]
=[..
1|. 1 .|-1 ..]*[. -Sa -Ca|. Ca -Sa|1 .. ]
=[1..|. Ca -Sa|. Sa
Ca]=[Rx(a)]
�@[Ry(90°)]*[Rz(a)]*[Ry(-90°)]=[Rx(a)] ��
| ��1/4��]1/4�Ђ˂聙 |
��1/4 ��] 1/4 �Ђ˂�@���]�����̂��̂���]����@���]�p���x�̑傫���ƁA���]�������̂��̂���]����p���x�̑傫����������
<�k��)=<.. 1)�@<�C���h)=<1 ..)�@<�����m)=<. 1 .)
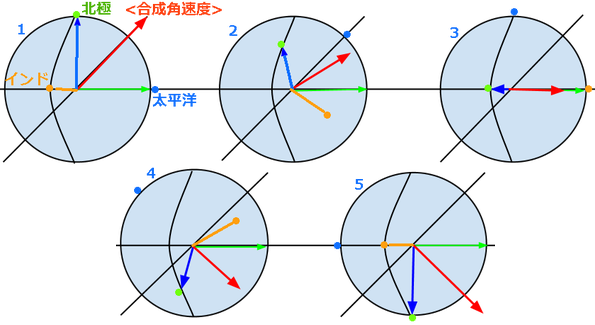
�����]�����̂��� z������Axz���ʂ���]����
��[���]��90°��]���āA���](�Ђ˂�)90°]=[Rx(90°)]*[Ry(90°)]
=[..
1|1 ..|. 1 .]
[���](�Ђ˂�)90°���āA���]��90°��]]=[Ry(90°)]*[Rz(90°)]
=[..
1|. 1 .|-1 ..]*[. -1 .|1 ..|.. 1]
=[.. 1|1 ..|. 1 .]
�@[���]��90°��]���āA���](�Ђ˂�)90°]
=[���](�Ђ˂�)90°���āA���]��90°��]] ��
{��}1�ڂ�2�ڂ̎��](�Ђ˂�)�̎����قȂ��Ă���{!}
���̂Ƃ��A\x=z�@\y=x�@\z=y
{�m����}<�k��)=<..
1) �� <1 ..)=<�C���h)
�@<�C���h)=<1 ..) �� <.
1 .)=<�����m)
�@<�����m)=<. 1 .) �� <.. 1)=<�k��)�@{�f���炵���I}
| ��1/2 ��] 1/2 �Ђ˂聙 |
��[Rx(180°)]=[1 ..|. -1 .|.. -1]
�@[Ry(180°)]=[-1 ..|. 1 .|.. -1]
�@[Rz(180°)]=[-1 ..|0 -1 .|.. 1]
��[���]��180°��]���āA���](�Ђ˂�)180°]=[Rz(180°)]*[Ry(180°)]
=[-1
..|0 -1 .|.. 1]*[-1 ..|. 1 .|.. -1]=[1 ..|. -1 .|.. -1]
�@\x=x�@\y=-y�@\z=-z�@yz���ʂł̓_�Ώ̈ړ�
�@<�k��)=<..
1) �� <.. -1)=<���)
�@<�C���h)=<1 ..) �� <1 ..)=<�C���h) �� �C���h�͖߂��ė���{!}
�@<�����m)=<.
1 .) �� <. -1 .)=<�A�t���J)
{�f���炵���A�����ƈ�v����!2013/1}