|
2015/11-2013/7 Yuji.W |
|
☆広義積分☆ |
◎ 元の関数が、ある所で発散していても、定積分を定義することができる{知らなかった。これが出てくるといつも、変だなあと思って終わっていた!2013/7}
☆ improper integral
〔表記〕ベクトル<> 座標単位ベクトル<xu>,<yu>,<zu> 内積* 外積#〔物理定数〕
微分 y;x 2階微分 y;;x 時間微分
y' 積分 ${f(x)*dx} 定積分
${f(x)*dx}[x:a~b]
累乗 ^ 10^x≡Ten(x) 1/x≡Over(x) exp(i*x)≡expi(x) 複素共役
z!
★.2015/11/13
| ☆広義積分 ?☆ |
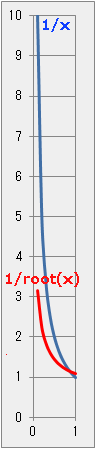 ◎
発散しているのに、積分値は存在するのか?
◎
発散しているのに、積分値は存在するのか?
◆ ${[1/root(x)]*dx}[x:0~1] 1/root(x) は x=0 で発散している(無限大になる)
一定の積分値を持つのだろうか ?
■ 0<Δx<<1 である Δx において、
Δx=0.1 のとき 1/root(Δx)~3.16
Δx=0.01 のとき 1/root(Δx)=10
Δx=0.001 のとき 1/root(Δx)~31.6
Δx=0.0001 のとき 1/root(Δx)=100
Δx が 0 に近づくにつれ、1/root(Δx) の値は大きくなる。
Δx->∞ で 1/root(Δx)->∞ 積分できない ?
${[1/root(x)]*dx}[x:Δx~1] という積分を考える。
積分の近似値
=[1/root(Δx)]*Δx+[1/root(2*Δx)]*Δx+[1/root(3*Δx)]*Δx+…
[1/root(Δx)]*Δx の値は、
Δx=0.1 のとき [1/root(Δx)]*Δx~3.16*0.1=0.316
Δx=0.01 のとき [1/root(Δx)]*Δx=10*0.01=0.1
Δx=0.001 のとき [1/root(Δx)]*Δx~31.6*0.001=0.0316
Δx=0.0001 のとき [1/root(Δx)]*Δx=100*0.0001=0.01
Δx が 0 に近づくにつれ、[1/root(Δx)]*Δx の値は小さくなる。
Δx->0 で [1/root(Δx)]*Δx->0 積分できる
----- まとめ -----
1/root(x) は、〔 x->0 で f(x)->∞ 〕ではあるのだが、
[1/root(Δx)]*Δx は、〔 Δx->0 で [1/root(Δx)]*Δx->0 〕であるので、次のように定義すれば、積分値を求める事ができる ★.
${[1/root(x)]*dx}[x:0~1]≡lim[h->0]{${[1/root(x)]*dx}[x:h~1]}
{普通は、以上のような説明がないまま、広義積分の話が進む。発散するのに積分値は存在する?モヤモヤが残ったまま進むから、わからなくなる!2015/11}
▲ Δx->0 のときに f(Δx) が大きくなる割合と、Δx が小さくなる割合の比較の問題になる。その大小によって、広義積分できる場合とできない場合がある。
例えば、1/x^2 は、x->0 のときに、Δx が小さくなる割合を超えて、急激に大きくなるので、x->0 まで広義積分できない。
■
${[1/root(x)]*dx}[x:0~1]
=lim(h->0){${[1/root(x)]*dx}[h:h~1]}
=lim(h->0){[2*root(x)][h:h~1]}
=lim(h->0){2-2*root(h)}
=2
≫ ${[1/root(x)]*dx}[x:0~1]=2 ★.
■
${[1/x^2]*dx}[x:0~1]
=lim(h->0){${[1/x^2]*dx}[h:h~1]}
=lim(h->0){[-1/x][h:h~1]}
=lim(h->0){-1+1/h}
->∞ 広義積分できない
★.
| ☆シミュレイション ${[dx/root(x)}[x:0~1]☆ |
).png) ◎
Excel を使って、広義積分 ${dx/root(x)}[x:0~1] を求めよう
◎
Excel を使って、広義積分 ${dx/root(x)}[x:0~1] を求めよう
■ 1/root(x) は、x=0 で発散する
${dx/root(x)}[x:0~1]=lim[h->0]{${dx/root(x)}[x:h~1]}
ステップ数 n 1/n=Δx として、次の値を求める。
I={1/root(Δx)+1/root(2*Δx)+1/root(3*Δx)+…+1/root(n*Δx)}*Δx
【 結果 】
n=10 I~1.63
※ ${dx/root(x)}[x:0.1~1]=2*[1-root(0.1)]~1.36
${dx/x}[x:0.1~1]=-ln(0.1)~2.30
n=100 I~1.86
※ ${dx/root(x)}[x:0.01~1]=2*[1-root(0.01)]~1.80
${dx/x}[x:0.1~1]=-ln(0.01)~4.61
n=1000 I~1.95
※ ${dx/root(x)}[x:0.001~1]=2*[1-root(0.001)]~1.94
${dx/x}[x:0.1~1]=-ln(0.001)~6.91
n=10000 I~1.99
※ ${dx/root(x)}[x:0.0001~1]=2*[1-root(0.0001)]~1.98
${dx/x}[x:0.1~1]=-ln(0.0001)~9.21
----- まとめ -----
${dx/root(x)}[x:0~1]=2 ${dx/x}[x:0~1]=発散してしまう
| ☆広義積分☆ |
■ x=b で発散している関数 f(x) に対して、${f(x)*dx}[x:b~c] を考える。
b<a<c となる値 a を選んで、発散しない範囲 a~c で、定積分を求める。
a->b の極限を求める。その極限値を、定積分の値とする。
${f(x)}*dx}[x:b~c]=lim[a->b]{${f(x)}*dx}[x:a~c]} ★.
その極限値が必ず有限の値をとるわけではない。発散してしまうこともある。
■ c で発散しているときも、同様に定義できる。
${f(x)}*dx}[x:a~∞]=lim[h->∞]{${f(x)}*dx}[x:a~h]} ★.
| ☆1/root(1-x^2)☆ |
| ● 0≦a<Pi/2 で sin(a) は単調増加関数 cos(a) は単調減少関数 その範囲で、両関数とも逆関数を定義できる。しかも、両関数とも、正の値しかとらない。 ● 0≦x<1 で ${[1/root(1-x^2)]*dx} を求めよう。 x=sin(a) と置く 0≦x<1 ⇔ 0≦a<Pi/2 dx=cos(a)*da root(1-x^2)=root[1-sin(a)^2]=root[cos(a)^2]=cos(a) ※ cos(a)≧0 だから ${[1/root(1-x^2)]*dx}=${cos(a)*da/cos(a)]}=${1*da}=a=arcsin(x) ≫ 0≦x<1 で ${[1/root(1-x^2)]*dx}=arcsin(x) |
◆ ${[1/root(1-x^2)]*dx}[x:0~1] 元の関数は x=1 で発散している 広義積分できる?
■
${[1/root(1-x^2)]*dx}[x:0~1]
=lim[h->1]{${[1/root(1-x^2)]*dx}[x:0~h]}
=lim[h->1]{[arcsin(x)][x:0~h]}
=lim[h->1]{arcsin(h)-arcsin(0)}
=arcsin(1)-arcsin(0)
=Pi/2-0
=Pi/2
★.
≫ ${[1/root(1-x^2)]*dx}[x:0~1]=Pi/2 ★.
| ☆1/root(A^2-x^2)☆ |
| ● 0≦x<A で ${dx/root(A^2-x^2)} を求めよう。 次のように置く x=A*X 0≦x<A 0≦X<1 dx=A*dX root(A^2-x^2)=A*root(1-X^2) ${dx/root(A^2-x^2)} ≫ ${dx/root(A^2-x^2)}=arcsin(x/A) |
◆ ${[dx/root(A^2-x^2)}[x:0~A] 〔A:正の定数〕元の関数は x=A で発散している
■ ${[dx/root(A^2-x^2)}[x:0~A]
=lim[h->A]{${dx/root(A^2-x^2)}[x:0~h]}
=lim[h->A]{[arcsin(x/A)][x:0~h]}
=lim[h->A]{arcsin(h/A)-arcsin(0/A)}
=arcsin(1)-arcsin(0)
=Pi/2-0
=Pi/2
≫ ${[dx/root(A^2-x^2)}[x:0~A]=Pi/2 ★.
|
〔A:正の定数〕 ${dx/root(A^2-x^2)}[x:0~A]=Pi/2 |
★ 広義積分 ★