☆ 積分.曲線の重心 ☆
〇 質量の中心 (1/4)*円 サイクロイド 2023.3-2017.11 Yuji.W ★
◇ 2*3=6 Ten(3)=10^3=1000 微分 ; 偏微分 : 積分 $ e^(i*x)=expi(x)
ベクトル <A> 縦ベクトル <A) 単位ベクトル <xu> 内積 * 外積 # 000
〓 曲線の重心 〓
◎ 線密度一定の細いひも
▢ xy平面 曲線 y=f(x) 〔x|x1~x2〕 曲線の長さ L 曲線の重心のy座標 Gy
曲線上の線分要素 dL=root(dx^2+dy^2)=root[1+(y;x)^2]*dx
▷ L=${root[1+(y;x)^2]*dx〔x|x1~x2〕}
L*Gy=${y*root[1+(y;x)^2]*dx〔x|x1~x2〕} ★
〓 曲線の重心-2- 〓
◎ パラメータ表示
▢ xy平面 曲線 x=f(a) , y=g(a) 〔a|a1~a2〕 曲線の長さ L
曲線の重心の位置 (Gx,Gy)
曲線上の線分要素 dL=root(dx^2+dy^2)=root[(x;a)^2+(y;a)^2]*da
▷ L=${root[(x;a)^2+(y;a)^2]*da〔a|a1~a2〕
L*Gx=${x*root[(x;a)^2+(y;a)^2]*da〔a|a1~a2〕} ★
L*Gy=${y*root[(x;a)^2+(y;a)^2]*da〔a|a1~a2〕} ★
〓 (1/4)*円 〓
▢ xy平面上に円 中心 原点 半径 1 その円の 1/4 の円周の重心 (Gx,Gy)
x^2+y^2=1 0<x<1 y>0 L=Pi/2
▷ x^2+y^2=1 x で微分して 2*x+2*y*(y;x)=0
y;x=-x/y=-x/root(1-x^2)
1+(y;x)^2=1+(-x/y)^2=(x^2+y^2)/y^2=1/y^2
dL=root[1+(y;x)^2]=1/y
y*dL=y*root[1+(y;x)^2]*dx=dx
L*Gy=${y*root[1+(y;x)^2]*dx〔x|0~1〕}=${dx〔x|0~1〕}=1 ★
Gy=1/L=1/(Pi/2)=2/Pi~0.64
同様に Gx=2/Pi~0.64
≫ 重心 (2/Pi,2/Pi) ★
〓 サイクロイド 〓
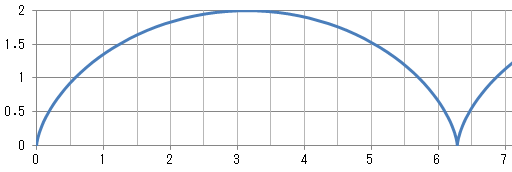
▢ 半径 1 の円が作るサイクロイド x=a-sin(a) y=1-cos(a) 〔a|0~Pi〕
0<x<Pi 0<y<2 重心のy座標 Gy
▷ x;a=1-cos(a) y;a=sin(a)
(x;a)^2+(y;a)^2=[1-cos(a)]^2+sin(a)^2=2*[1-cos(a)]=4*sin(a/2)
dL=root[(x;a)^2+(y;a)^2]*da=2*sin(a/2)*da
▷ L=${dL〔a|0~Pi〕}
=2*${sin(a/2)*da〔a|0~Pi〕}
=-4*${cos(a/2)〔a|0~Pi〕}
=4
L=4 ★
▷ L*Gy
=${y*dL〔a|0~Pi〕}
=2*${[1-cos(a)]*sin(a/2)*da〔a|0~Pi〕}
● cos(a)*sin(a/2)=(1/2)*[sin(3*a/2)-sin(a/2)] ●
[1-cos(a)]*sin(a/2)
=sin(a/2)-(1/2)*[sin(3*a/2)-sin(a/2)]
=(3/2)*sin(a/2)-(1/2)*sin(3*a/2)
L*Gy
=${[3*sin(a/2)-sin(3*a/2)]*da〔a|0~Pi〕}
={-6*cos(a/2)+(2/3)*cos(3*a/2)}〔a|0~Pi〕}
=0-(-6+2/3)
=16/3
L*Gy=16/3 ★
▷ Gy=(L*Gy)/L=(16/3)/4=4/3 ★
▲ サイクロイド1周期分の重心の座標 (Pi,4/3) ★
☆ uzお勉強しよう since2011 Yuji.W