☆ 指数関数 ☆
◎ ★_
【数学】ベクトル <A> 単位ベクトル
<-u> 内積
* 外積 #
10^x=Ten(x) 虚数単位 i ネイピア数
e e^(i*x)=expi(x) 微分
; 積分 $
行列 [A]=[a b|c d] テンソル〚〛
〓 ネイピア数 〓
■ ネイピア数 e=lim[x->0]{(1+x)^(1/x)} または e=lim[x->∞]{(1+1/x)^x}
2.71827<e<2.71830
■ lim[x->0]{ln(1+x)/x}=1 lim[x->0]{(e^x-1)/x}=1
■ xによる微分 (e^x);x=e^x (a^x);x=ln(a)*a^x
〓 指数法則 〓
■ 2^3*2^4=2^7 (2*5)^3=2^3*5^3 (2^3)^2=2^6
■ a^m*a^n=a^(m+n) (a*b)^m=(a^m)*(b^m) (a^m)^n=a^(m*n)
※ a,b,m,n は、整数のみならず、複素数まで拡張できる
〓 指数関数 〓
◆ ネイピア数 e e^x=exp(x)
■ exp(0)=1 exp(1)=e~2.7 exp(2)=e^2~7.3 exp(3)=e^3~19.7
exp(-1)=1/e~0.37 exp(-2)=1/e^2=0.14 exp(-3)=1/e^3~0.05

■ 任意の値 x x~x+1 の値の比を調べる
exp(x+1)/exp(x)=exp(x)*e/exp(x)=e~2.7
x が 1 増えると、exp(x) は、e~2.7 倍になる〔★〕
exp(-x) なら、x が 1 増えると、exp(-x) は、1/e~0.37 倍になる〔★〕
{わかってなかったなあ!2014/8}
■ x~x+Δx で、exp(x) が、2倍になるとしよう。
2=exp(x+Δx)/exp(x)=exp(Δx)
Δx=ln(2)~0.7 ※ ln(2)~0.7 は e^0.7~2 という意味
x が 0.7 増えると、exp(x) は 2倍になる。exp(-x) は 1/2 になる〔★〕
■ 時間 t 定数 T exp(t/T)
t が T 増えるごと、exp(t/T) は e倍になり、ln(2)*T 増えるごと 2倍になる
t が T 増えるごと、exp(-t/T) は 1/e 倍になり、ln(2)*T 増えるごと 1/2倍になる
ln(2)*T~0.7*T を半減期と呼ぶ
■ exp(x) と ln(x) とは逆関数同士だから、
a=exp[ln(a)]〔★〕
{あたりまえ過ぎて、忘れてしまう。暗記すべき!2014/1}
★ 3=exp(ln3)~e^1.10 10=exp(ln10)~e^2.30
2=exp(ln(2))=e^0.69
■ さらに a^x={exp[ln(a)]}^x=exp[ln(a)*x]〔★〕{使えるようにすべき!}
★ 3^x=exp(ln3*x)~exp(1.10*x) 10^x=exp(ln10*x)~exp(2.30*x)
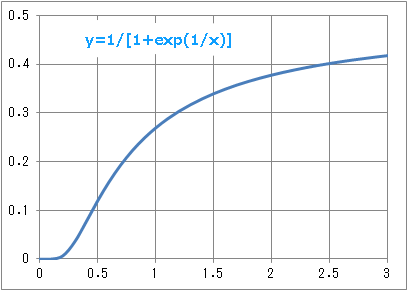
〓 1/[1+exp(1/x)] 〓
|
x |
0.1 |
0.5 |
1 |
1.5 |
2 |
2.5 |
3 |
∞ |
|
1/[1+exp(1/x)] |
0 |
0.12 |
0.27 |
0.35 |
0.38 |
0.40 |
0.42 |
0.5 |
■
〓 近似式 〓
■ |x|<<1 のとき exp(x)=1+x
■ f(x)=2^x ln[f(x)]=ln(2)*x x で微分すると、
左辺=[f(x);x]/f(x)=[(2^x);x]/2^x 右辺=ln(2)
[(2^x);x]/2^x=ln(2)
(2^x);x=ln(2)*2^x~0.693*2^x ★
|x|<<1 のとき 2^x=2^0+x*ln(2)*2^0=1+ln(2)*x ★
|
■ |x|<<1 のとき exp(x)=1+x 2^x=1+ln(2)*x (1/2)^x=1-ln(2)*x |
★ 2^0.1~1.072 1+ln(2)*0.1=1.069
2^0.01~1.00696 1+ln(2)*0.01=1.00693
★ exp(0.1)~1.105 1+0.1=1.1
★ exp(0.01)~1.01005 1+0.01=1.01
★ exp[5*Ten(-3)]~1.00501 exp[5*Ten(-3)]=1+5*Ten(-3)=1.005
■ 定数 A 2<x のとき exp[A*Ten(-x)]=1+A*Ten(-x)
〓 exp(x) と Ten(x) 〓
◇ e^x=exp(x) 10^x=Ten(x)
◎ exp(x) から Ten(x) を求める
● e~2.7183 ln(2)~0.69315 ln(10)~2.3026
■ Ten(x)/exp(x)=(10/e)^x
対数をとると、
ln[Ten(x)]-ln[exp(x)]=x*[ln(10)-ln(e)]
ln[Ten(x)]-x=x*[ln(10)-1]
ln[Ten(x)]=x*ln(10)
Ten(x)=exp[x*ln(10)] ★.
★ root(10)=Ten(0.5)=exp(0.5*2.3026)=exp(1.1513)~3.1623
3.1623^2~10.0001
■ |x|<<1 のとき exp(x)=1+x
Ten(x)=exp[x*ln(10)]=[exp(x)]^ln(10)=(1+x)^ln(10)=1+x*ln(10) ★.
■ |x|<<1 のとき exp(x)=1+x
両辺の対数をとると x=ln(1+x)
また LOG(1+x)=ln(1+x)/ln(10)=x/ln(10)
|
● e~2.7183 ln(2)~0.69315 ln(10)~2.3026 ■ Ten(x)=exp[x*ln(10)] ■ |x|<<1 のとき exp(x)=1+x Ten(x)=1+x*ln(10) ln(1+x)=x LOG(1+x)=x/ln(10) |
■
〓 指数関数の概数 〓
【 底 10 の対数関数 LOG 底 e の対数関数 ln 】
◎ exp(x) の概数が知りたい
● ln(x)=ln(10)*LOG(x)~2.303*LOG(x)
■ LOG[exp(x)]=ln[exp(x)]/ln(10)=x/ln(10)~x/2.303
exp(x)=10^[x/ln(10)] ★ {これ使える!2015/8}
|
■ exp(x)=10^[x/ln(10)] |
★ exp(3)~20.1 exp(3)~10^(3/2.303)~10^1.3 > 10
★ exp(10)~22026 exp(10)~10^(10/2.303)~10^4.3 > 10000
★ exp(-5)~0.0067
exp(-5)~10^(-5/2.303)~10^(-2.2)~1/10^(2.2) < 1/100