☆ 微分.極限-2- ☆
〇 極限 2023.5-2013.10 Yuji.W ★
◇ 2*3=6 Ten(3)=10^3=1000 微分 ; 偏微分 : 積分 $ e^(i*x)=expi(x)
ベクトル <A> 縦ベクトル <A) 単位ベクトル <xu> 内積 * 外積 # 000
〓 数学での微分の意味 〓
〇 変数 x x の関数 y(x) lim{h->0 y(x+h)-y(x)}=0 となるとき、
lim{h->0 [y(x+h)-y(x)]/h}=0/0 ? ではなく、
lim{h->0 [y(x+h)-y(x)]/h}=(ある値) となる場合がある。
このとき、その値を、「微分」、「微分係数」と言い dy/dx と表す。
微分は、変化の割合、傾きを表す。
※ 極限値は h->∞ でもよい。
〓 {例}極限値 〓
|
|
0.5 |
0.1 |
0.01 |
x→0 |
|
sin(x)/x |
0.958 |
0.998 |
0.999 |
1 |
|
sin(3*x)/x |
1.994 |
2.955 |
2.999 |
3 |
|
[1-cos(x)]/x |
0.245 |
0.050 |
0.005 |
0 |
|
[exp(x)-1]/x |
1.297 |
1.051 |
1.005 |
1 |
|
x*ln(x) |
-0.346 |
-0.230 |
-0.046 |
0 |
{こういう計算をしないと、極限の意味はつかめない!高校の時にこういう計算を少しでもすれば、もっとよくわかったのに!2014/1}
〓 lim{x→+0 x^x} 〓
▢ x>0 lim{x→+0 x^x} lim{x→+0 x*ln(x)}
▷
|
x |
0.01 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
|
x^x |
0.95 |
0.79 |
0.72 |
0.70 |
0.69 |
0.70 |
0.74 |
0.78 |
0.84 |
0.91 |
1 |
|
x*ln(x) |
-0.05 |
-0.23 |
-0.32 |
-0.36 |
-0.37 |
-0.35 |
-0.31 |
-0.25 |
-0.18 |
-0.09 |
0 |
lim{x→+0 x^x}=1 ★ lim{x→+0 x*ln(x)}=0 ★
{不思議!知らなかった!2016/7}
〓 x*ln(x) x^x x*ln(x)+(1-x)*ln(1-x) 〓
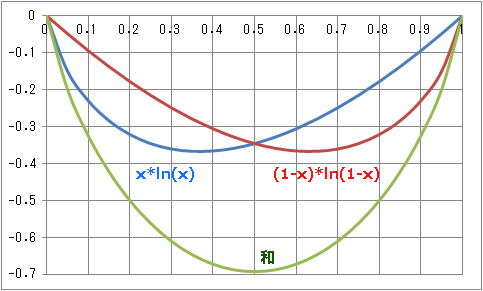
▢ x*ln(x) x^x x*ln(x)+(1-x)*ln(1-x) 最小値
▷ [x*ln(x)];x=ln(x)+1
ln(x)+1=0
ln(x)=-1
x=exp(-1)=1/exp(1)=1/e=1/2.7183~0.37
そのとき (1/e)*ln(1/e)=-1/e~-0.37
[x*ln(x) の最小値]=(1/e)*ln(1/e)=-1/e~-0.37 ★
▷ (x^x の最小値)=(1/e)^(1/e)=exp(-1/e)~0.69 ★
▷ [x*ln(x)+(1-x)*ln(1-x) の最小値]=2*(1/2)*ln(1/2)=-ln(2)~-0.69 ★
☆ uzお勉強しよう since2011 Yuji.W