数学　2021.7-2011　Yuji.W

〇 cycloid　タイヤが道路と接する点にしるしをつける。タイヤを転がす。しるしが動いた軌跡を「サイクロイド」と言う。　★　

0.お勉強　A.力学　B.特殊相対性理論,電磁気　C.物理学一般　D.数学,その他　E.Python

000　py-　0table-202012

2*3=6　6/2=3　3^2=9　1000=10^3=Ten(3)　
微分 :　偏微分 ;　積分 $　ネイピア数 e　虚数単位 i　e^(i*x)=expi(x)
ベクトル <A>　縦ベクトル <A)　単位ベクトル <Au>　内積 *　外積 #　　2021.7

〓　床を転がるサイクロイド　〓　

 ◇ 半径 1 の円によるサイクロイド

半径 1 の円をx軸上で転がし、右側に移動させる。円は右回りである。円周上の1点の軌跡を考える。

回転角 a_rad　水平 x軸　高さ y軸　a=0 のとき 原点

　a:0~2*Pi　x:0~2*Pi　y:0~2

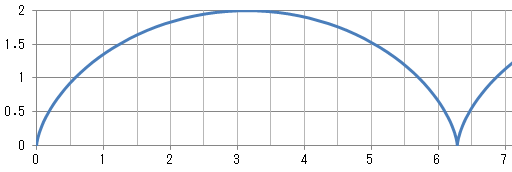
■ x,y は、回転角 2*Pi ごとの周期関数。cos(a) , sin(a) の関数。

■ 円の中心は、高さ 1 を保ったまま、右側に水平に動く。a_rad だけ回転すれば、a だけ移動する。

　円の中心の位置 (a,1)

円の中心から見た、円周上の1点の座標 (-sin(a),-cos(a))

円周上の1点の座標　x=a-sin(a)　y=1-cos(a)　★　

■ 0<a<<1　のとき　x=a-a=0　y=1-1=0　動かない

cos(a)=1-a^2/2　と近似すると　y=1-[1-a^2/2]=a^2/2　上向きに動き出す

■ a~Pi　のとき　x~Pi　y~2

▲ 半径 R の円の場合　x=R*[a-sin(a)]　y=R*[1-cos(a)]

※ すべてのサイクロイドは相似。ある1つの決まった形。それは、円や放物線と同様。

〓　上下反転したサイクロイド　〓　

◇ 半径 1 の円によるサイクロイド　y軸で上下反転　y軸下向きを正

　x=a-sin(a)　y=1-cos(a)

〓　いろいろなサイクロイド　〓　

◇ 半径 1 の円によるサイクロイド　※ すべて合同

■ A 床(y=0)を右側に転がる　円は右回り　a=0 のとき x=0 , y=0

■ B 天井(y=2)に張り付いて右側に転がる　円は左回り　a=0 のとき x=0 , y=2

■ C　天井(y=2)に張り付いて右側に転がる　円は左回り　a=0 のとき x=0 , y=0

※ C は B の右側にくっつくと考えてもよい

■ D 床(y=0)を右側に転がる　円は右回り　a=0 のとき x=0 , y=2

※ D は A の右側にくっつくと考えてもよい

〓　天井に張り付いて転がるサイクロイド　〓　

◇ グラフB　半径 1 の円が天井(y=2)に張り付いて右側に転がる　円は左回り

 a=0 のとき x=0 , y=2

■ 円の中心は、高さ 1 を保ったまま、右側に水平に動く。a_rad だけ回転すれば、a だけ移動する。

　円の中心の位置 (a,1)

円は左回り　円の中心から見た、円周上の1点の座標 (-sin(a),cos(a))

円周上の1点の座標　x=a-sin(a)　y=1+cos(a)　★　グラフB

★ a=Pi/2 のとき、

　x=Pi/2-sin(Pi/2)~1.57-1=0.57　y=1+cos(Pi/2)=1+0=1　(0.57,1)

★ a=Pi のとき、

　x=Pi-sin(Pi)~3.14-0=3.14　y=1+cos(Pi)=1-1=0　(3.14,0)

◇ グラフC　半径 1 の円が天井(y=2)に張り付いて右側に転がる　円は左回り

 a=0 のとき x=0 , y=0

■ グラフB において、a=Pi が始点になるようにし、グラフを左側に Pi だけ平行移動すればよい。

　x=a-sin(a)　⇒　x+Pi=(a+Pi)-sin(a+Pi)　⇒　x=a+sin(a)

　y=1+cos(a)　⇒　y=1+cos(a+Pi)　⇒　y=1-cos(a)

≫　x=a+sin(a)　y=1-cos(a)　★　グラフC

★ a=Pi/2 のとき、

　x=Pi/2+sin(Pi/2)~1.57+1=2.57　y=1-cos(Pi/2)=1-0=1　(2.57,1)

★ a=Pi のとき、

　x=Pi+sin(Pi)~3.14+0=3.14　y=1-cos(Pi)=1+1=2　(3.14,2)

〓　いろいろなサイクロイド　〓　

〇 半径 1 の円によるサイクロイド　※ すべて合同

 　A  x=a-sin(a) , y=1-cos(a)    B  x=a-sin(a) , y=1+cos(a)

 　C  x=a+sin(a) , y=1-cos(a)    D  x=a+sin(a) , y=1+cos(a)

☆ お勉強しよう　since 2011　Yuji Watanabe